結界が菱形ということで菱形と神を検索中見つけたのが古神道で出てくる立方体の理論。
古神道では空間を立方体で表しこの立方体の連続が全空間だと考える。
菱形はこの立方体を2次元であらわしたもので、たとえば武田菱や菱紋などはここから来ている。
ここから菱形が連続している模様は空間だと考えることができるのだが、今回できた結界を菱形(平行四辺形)だと考え、これが連続しているとすれば結界の外のポイントも同じ菱形に重ね合わせて中央の菱形に位置を移動することができる。
複雑だがいかにも理科系のV3w氏が考えそうなアイデアだ。
まず地図に結界の大きさの平行四辺形を網目のように敷き詰めていく、その後できた平行四辺形に対してどの位置にポイントがあるかをチェックして中央の菱形の部分に平行移動する。
人呼んで<V3wの網タイツ理論>!! (^^)
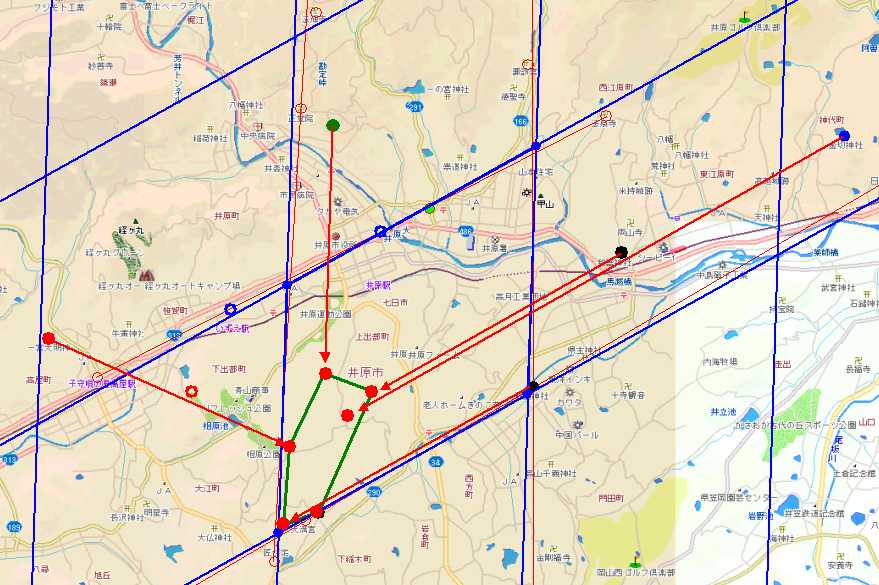
これを実施すると全てのポイントが結界の左下あたりにくる。
そしてこのポイントに囲まれた部分(緑の線に囲まれた部分)にある市の施設といえば相原公園キャンプ場と最初に探した山王日吉神社の近くの給水塔。
中央のポイントは山王公民館と祠のあたり。
結界は宝をあらわしだから宝の側には菱形模様のフェンスがあるのかもしれない。
探索に行ってみる。
相原公園キャンプ場の甲寅方向にある菱形フェンスと木のまわり、そして給水塔の周りにある菱形フェンスの周辺をもう一度調べたがそこにも無し。
いずれも隠せそうなところがあまりない。
そもそも地図にこんな面倒くさいことをしろというのがおかしい気がしてきた。
誰でもできないじゃん。
前述の最短距離理論の方がずっともっともらしい。(T.T)
その他に「方違え理論」・「六芒星理論」も考えたがどれもうまくいかない
しかしそれにしても手詰まりの状態だ。
道路脇にでも宝があるんだろうか?